Page 31 - El Modelo de Regresión Lineal

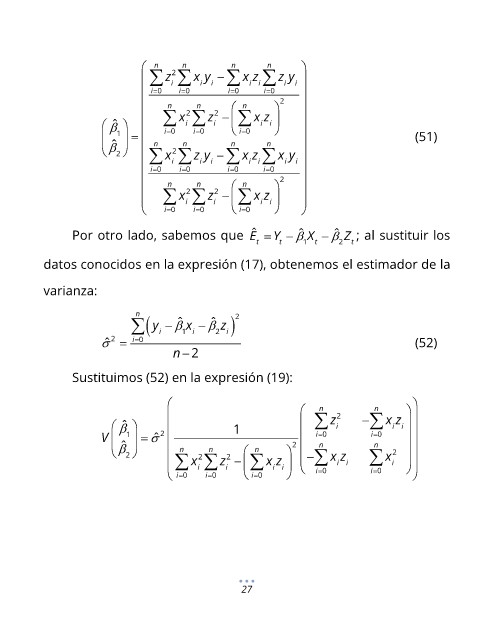
 n 2 n n n 
i 
i i
 z i  x y − x z z y i  
i
i
 i= 0 i= 0 i= 0 i= 0 
 n n  n  2 
i i 
2
  x 2 z −  x z 
   i i   
ˆ 
  1  =  i= 0 i= 0 i= 0  (51)
ˆ 
n
n
i 
    x i  z y − n x z n x y 
i i
2 
2
 i= 0 i= 0 i i= 0 i= 0 i i 
 n n  n  2 
i i 
  x 2 z −  x z 
2
 i i 
 i= 0 i= 0  i= 0  
ˆ
Por otro lado, sabemos que E = Y −  ˆ X −  ˆ Z ; al sustituir los
t t 1 t 2 t
datos conocidos en la expresión (17), obtenemos el estimador de la

varianza:

n 2
(  y − i  ˆ 1 i  ˆ 2 i )
z
x −
2
ˆ  = i= 0 (52)
n − 2

Sustituimos (52) en la expresión (19):

 n n 
i i  
  z 2 −  x z  
   1  i 
ˆ 
V  1  = ˆ  2   i = 0 i = 0  
  2  n n 
ˆ 
 2   n 2 n 2  n  − x z  x i   2 
i i 
  x i z −  x z   i i  
i
 i= 0 i= 0  i= 0  i = 0 i = 0 

27